October 15, 2025
A Delicious Free Lunch: Better Projections Improve ColBERT

TLDR:
ColBERT models are amazing retrievers, but a lot of their mechanisms are understudied. We show that MaxSim's unique constraints have strong implications for model training and focus on one that makes a single-layer projection suboptimal. We introduce a variation of new projection heads to ColBERT and achieve great performance through this simple modification. For more details, read our arXiv pre-print or try it out by training a model, with these new variants already supported in PyLate.
Introduction
We all know the story by now: after ChatGPT, RAG became all the rage. With the rising interest in RAG, Information Retrieval as a field then saw an unprecedented level of attention. And with this wave of interest, the broad concept of semantic retrieval built on top of language models, which was previously an active-but-somewhat-niche subject, became a mainstream topic.
In addition to single-vector retrieval, the most basic form of semantic matching where both queries and documents are represented as a single vector, many interesting research avenues enjoyed their well-deserved time in the spotlight: among them, sparse retrieval (SPLADE) and, of course, our preferred method: multi-vector retrieval, spearheaded by ColBERT.
Without straining your attention raving about ColBERT for the millionth time, let's have a quick reminder: ColBERT-inspired models, a.k.a. late-interaction methods, a.k.a. multi-vector retrieval (yes, there are too many names), are a family of retrieval models which rely on the idea that fine-grained interactions are very important for retrieval. To acknowledge the reality that inference-time is naturally sensitive in search settings, these models make fine-grained interaction possible by representing documents as bags-of-vectors rather than as a single vector: each individual token in both queries and documents are represented by their own individual vector, which then goes through heavy compression to avoid ballooning storage costs. You may read more about how ColBERT models perform scoring in our blog on MaxSim, their key scoring operator.
Recently, late interaction models have scored many wins. They've been shown to be state-of-the-art on all kinds of multimodal retrieval situations, far above any other retrieval paradigm, showcased their ability to generalise from being trained on short, 300-token documents to retrieve long, 32000-token documents, far better than even models specifically trained for it, and have they have demonstrated that they can match models with orders of magnitude more parameters.
Now, I know what you're thinking. Is this just another Big Multi-Vector lobbying blog post? Are you writing this introduction just to tell us that ColBERT is all we need? Honestly, yes, but not only. I'm writing this introduction to point out that despite going from empirical win to empirical win, we still understand very little of the mechanics that make late-interaction work. There are many factors to the performance of these models which have simply not yet been studied, and in this blog post we will focus on one of them to show how a simple solution can increase performance with virtually no trade-offs.
Learning Properties You Might Not Have Thought About
As mentioned above, multi-vector models perform scoring via the MaxSim operator. Without going too far into the details, it works through a simple process:
- For every token within a query, compute its cosine similarity with every token within a document.
- Discard all resulting similarity scores, except the highest for each query token.
- Sum these similarities: Voilà! That is your MaxSim score for this query < > document pair
- Repeat for every document you want to score.
During real-world retrieval scenarios, this score is used to order documents from most to least relevant. During training, it's used for loss calculation, whether through some form of contrastive loss (maximizing the score of positive examples and minimizing that of negative ones) or knowledge distillation (attempting to match the teacher's score distribution).
In the training setting, however, this operator results in an effect you might not necessarily have thought of: it zeroes out the vast majority of gradients, with gradients flowing only through tokens which have achieved the highest simiarity with at least one query token. If you are training with a document length of 512 and your queries are just 8 tokens long, that means that, in the best case scenario, 1.5625% of your document tokens will actually contribute to updating your model's weights (if you are lucky, that is, because it might well be the case that multiple query tokens are best matched with the same document token!).
There is a lot to be said about this mechanism: could it be one of the reasons that ColBERT performs so well, because it allows hyper-specialization and reduces noise during training? Or is it actually a harmful signal bottleneck, just waiting to be alleviated to unleash an even more glorious era of late interaction upon us?
The definite answer to this question is not to be found in this blog post, however, we do think that it means one thing...
Single-Layer Linear Projections Considered Harmful
And that thing is: the projection head of ColBERT models is likely suboptimal. If you aren't familiar with it, all existing multi-vector retrieval models end with a single layer, which is added to whatever backbone model is used (historically, BERT, and more recently, PaliGemma, Qwen, ModernBERT...) to downcast the model's final token representations to a much more manageable dimension, usually set to 128 by convention following the original ColBERT model.
We think that this projection is suboptimal and that it's partially related to the effects of MaxSim on learning. To be perfectly honest with you, both the paper (and its dozen equations!) and this blog post are actually somewhat back-engineered to understand exactly why a simple projection isn't good enough after empirical results demonstrated it.
The reason for this, we believe, is that ultimately a single-layer projection is just a mapping, without much learned in the process. And that is because a simple fact of the way MaxSim works and affects learning is that it rewards high peaks: you want particularly discriminative tokens to score very high in similarity to query tokens, as all other tokens will then not matter anymore.
While this might be stating the obvious, the problem here is that tokens are different from one another. What I mean by that is that different token types will quite naturally have differing representations in the embedding space: entities, e.g. proper nouns, are likely to be pretty different from adjectives, which are going to be pretty different from highly-specialised medical vocabulary, and so on.
But this is badly aligned with a single projection matrix! By definition, if you want to project from a big fixed dimension to a smaller fixed dimension and you must do so with a single learned mapping, then this mapping will have to "distribute" its weight budget in a way that covers all kinds of token types more or less equally well. In doing so, it weakens the representations' abilities to achieve high peaks in the first place because some sharpness is lost in the projection process.

If you remember only one thing from this session, let it be this framing.
Do bear in mind that while I make it sound dramatic, as is customary when introducing a slightly better variant of something, in practice, a single-layer projection does retain a good level of representation quality, and parts of the potential harmfulness are alleviated by the backbone model's expressiveness. Nonetheless, the fact that good enough exists doesn't mean that there aren't simple ways to make things better.
Better Projections Are Possible
And it is indeed possible to make things better, in a rather straightforward way! Building on the limitations highlighted above, we propose a bunch of justifications (that you can, again, find in the paper) as to why we believe that additional projection depth could considerably improve sharpening, thanks to factorization better spreading the mapping, and for adding residual connections to better leverage the quality of the original representations. We also discuss the potential impact of gating (GLU) and non-linearities and show that their theoretical impact is unclear, as they seem to introduce both beneficial and harmful properties.
We then set out to demonstrate how these properties hold up in practice: as always in deep learning, empirical results are king. As part of our experiments, we modified the excellent PyLate ColBERT training library to add a few knobs:
- Projection Depth: How many layers the projection should use.
- Projection Scale: Whether intermediate layers should be up-scaled (similarly to the Transformers' feedforward upscaling) or not.
- Activation Function: Which activation, if any, should be applied to the output of non-final layers.
- GLU Gating: Whether to use GLU modules or traditional feedforward modules.
- Skip-connections: Whether we should use residual connections for intermediate layers (note: in case of depth=2, we use ResNet-inspired residuals, where a second up-projection initialized with an identity matrix is used to upcast the residual)
The above is a non-exhaustive list, and you may find more information in our pre-print if you care about the full experimental setting.
With these knobs in place, we set out to train a few hundred models, with all other settings kept identical between runs. We trained each variant multiple times, with a few random seeds, in order to ensure significance, as it's previously been shown that it is fairly common for new QA retrieval state-of-the-art-results to actually fall behind existing methods when properly controlling for multiple seeds.
If you will allow me, here is everyone's favourite money-shot, the LaTeX booktab table with best results in bold and the infamous significance dagger:
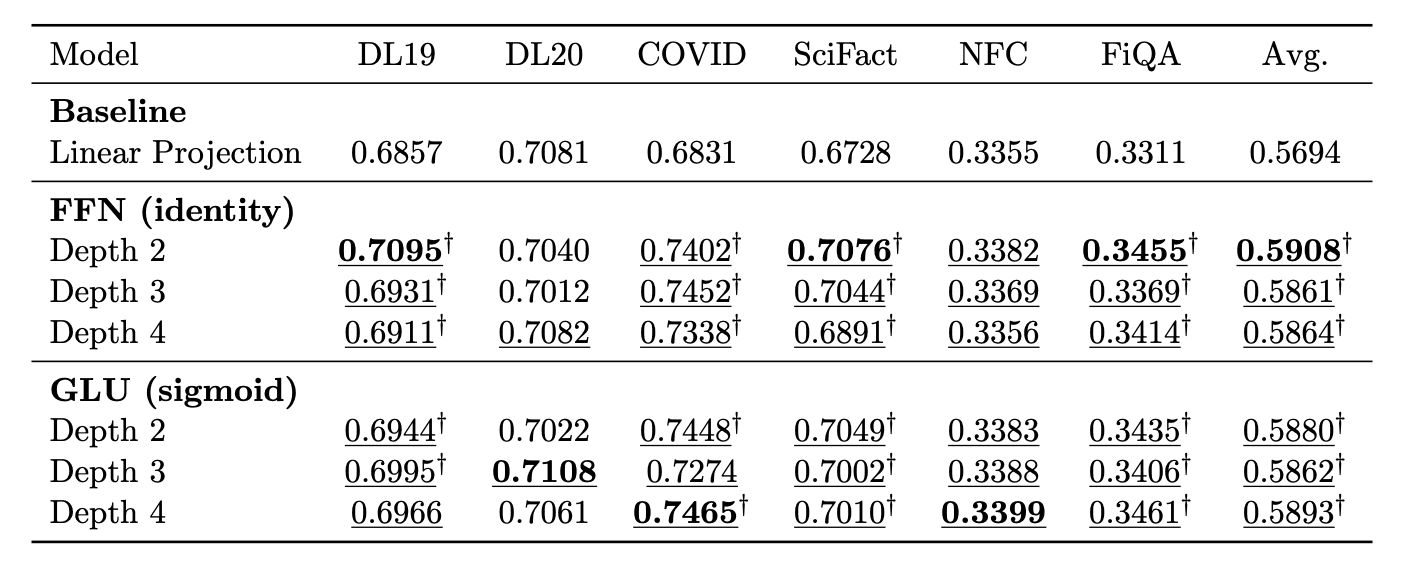
Table 1: Main results from our projection variant ablation study.
What we find is that almost all projection variants in this table show significant gains over the existing projection method, across multiple datasets. Note that this table is somewhat cherry-picked, as it presents the best performing "model families", employing both residuals and upscaling. Our broader results, however, show that the majority of projection variants do significantly improve retrieval performance, with the best ones reaching a rather comfortable 2 NDCG@10 points increase in average, representing an almost 4% relative improvement, at virtually no cost whatsoever except a few dozen thousand parameters.
Conclusion
Our results align with our original thought: while this, in itself, is not a revolutionary improvement, it is a consistent gain which highlights that there are likely many more low-hanging fruits to be discovered as we focus on better understanding the mechanisms of late-interaction.
If doing so is something that is interesting to you, we are currently hiring across all positions:
- Research: Research Staff, and Research Interns
- Software: Software Engineer, Frontend Engineer and DevOps Engineer
- Product: Product Designer
This is the first post in our Fast Rising Science series: at Mixedbread, we conduct a lot of experiments in various aspects of Information Retrieval. We think it's a shame how much science, especially in this space, is conducted entirely behind closed doors, with the same results often being re-discovered multiple times within the same year. We intend to frequently release focused research into these small-but-important mechanisms in the future.