maxsim-cpu: Maximising Maxsim Efficiency

In retrieval world, a lot of inference pipelines run on CPU: oftentimes because of cost optimization: CPU machines are pretty cheap and infinitely scalable. In a lot of cases, it's not even an optimization: if you're running a local retrieval pipeline, your laptop might not even have a GPU! In most cases, thankfully, CPUs can do a more-than-acceptable job for the typical retrieval workflow, where the only computations required are a single inference pass on a query followed by similarity calculations.

However, the equation is a bit different when it comes to multi-vector retrieval, which powers late-interaction models such as ColBERT or ColPali. These models use the MaxSim operator, which requires considerably more computations than their single-vector counterparts (read on to know why!).

While modern hardware thankfully makes this pretty fast, the additional computational cost adds up: running MaxSim on ~1000 documents with PyTorch on CPU can add between 50 and 100 milliseconds to each query compared to running it on GPU: while this may seem rather small at first glance, inefficiencies add up, and spending so much time on distance calculation can make it unviable for many latency-sensitive environments.

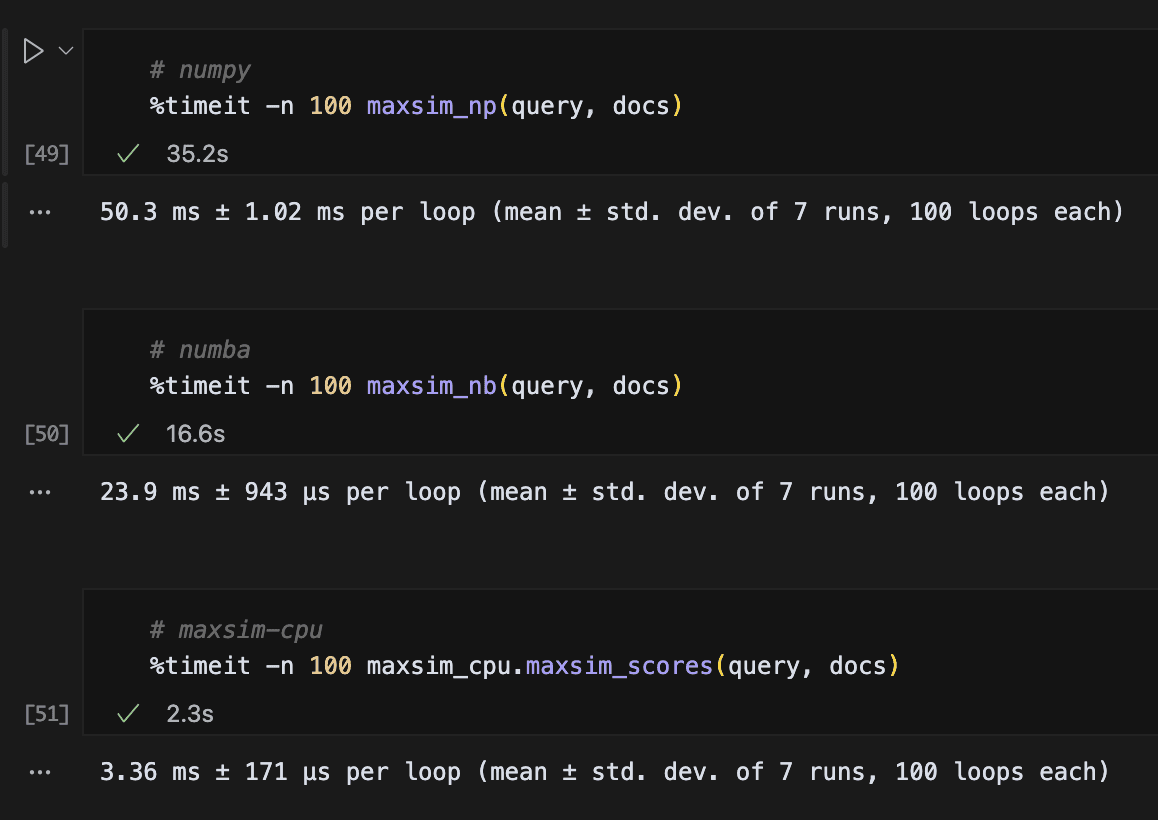
But it doesn't have to be this way! Obviously, current CPUs will never be as fast as GPUs for this sort of computation, but they don't have to be so slow! By taking advantage of architecture-specific instructions and low-level scientific computing libraries like libxsmm, we built maxsim-cpu: a small Python package, written in Rust, which cuts down the aforementioned overhead to just 5 milliseconds.

Want to just jump in and try it out? Check out our GitHub repo or install the library directly:

[uv] pip install maxsim-cpu

Want to understand a bit more about why it's useful? Read on!

What even is MaxSim?

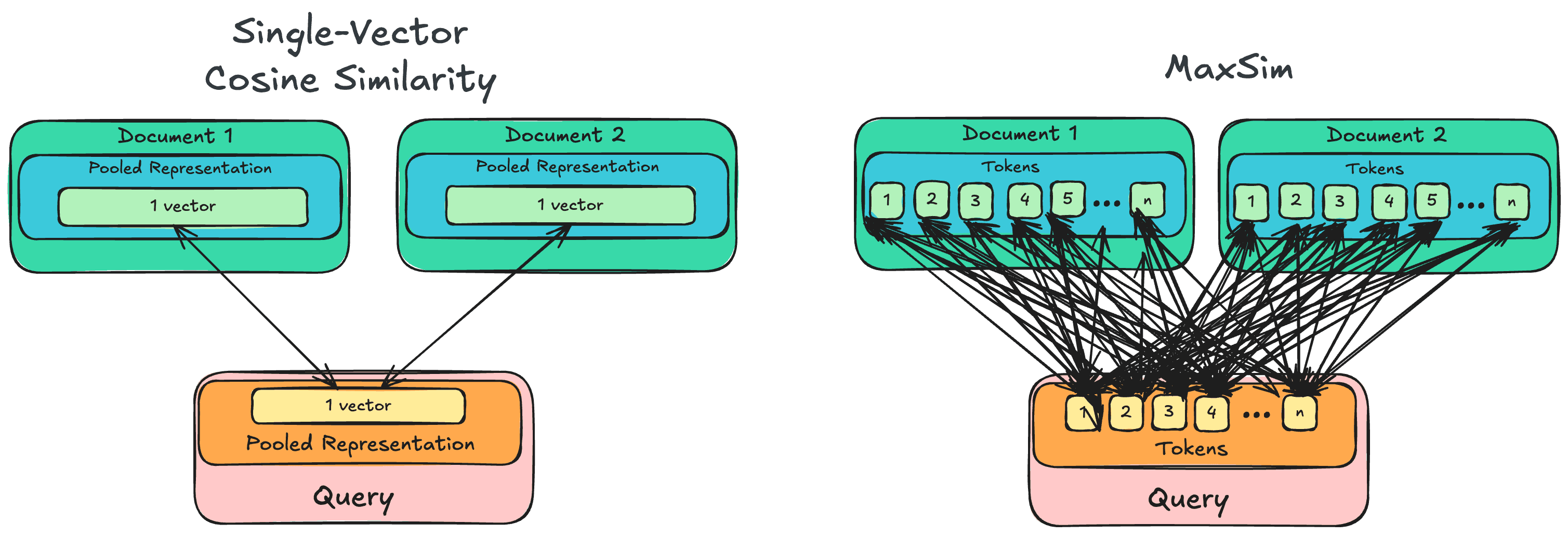
MaxSim, or for Maximum Similarity is the core element of current late-interaction models ColBERT, ColPali.... Its mechanism is simple: rather than performing a single cosine similarity computation between a vector representing the whole query and vectors representing entire documents, it computes token-level similarities.

For each candidate document, MaxSim iterates through every token within the query, and compares its similarity to every token within the document, before keeping the maximum value for each query token (hence the Max) and summing them up to produce a document-level score.

Orders of Magnitudes Matter

This approach has many benefits: it allows for capturing semantic relationships that larger-grain methods would miss. But it is inefficient: for each query, it requires thousands of similarity calculation. For a simple example: given 1000 candidate documents, each containing 300 tokens, and a 32-token long query , a "traditional" single-vector query search query would perform 1000 cosine similarity calculation: one for each document against the query. Using MaxSim, we require n_query_token * n_docs * n_token_per_doc distances, or 32 * 1000 * 300 = 9 600 000 (yes, that's 9.6 millions) distance calculations.

How is it viable, then? Well, thankfully, cosine similarity calcualtions are very computationally cheap. In fact, with normalized vectors (which everyone uses), it's a simple matrix multiplication. As you might know if you've ever looked at the math behind deep learning, matrix multiplications are the main computational operation that power all models, and GPUs are very, very good at running them quickly. This, compounded by the fact that individual vectors generated by ColBERT models are pretty small, means that the computational cost is pretty cheap: in fact, it's less half the compute required to run a forward pass through a single layer of BERT-base, something that any GPU released in the last decade can do in a handful of milliseconds.

The Problem

So, there's no problem then? Well, not really. GPUs love matrix multiplications and parallel computation, that's what they're built for: thousands of really weak cores. Their trustworthy cousin, the humble CPU, is not quite as big a fan of this sort of workload.

This results in the situation we mentioned in the introduction: computing MaxSim on CPU can quite often be a significant source of latency in retrieval systems. While the FLOPS required to perform these computations is relatively low, from the CPU's point of view, they're the most evil FLOPS there are: a lot of very small parallel computations. What CPUs enjoy is the complete opposite, they love performing big, more demanding computations that don't require so many tiny steps.

But CPU machines are very, very cheap and widely available. So, many pipelines end up just having to take that latency hit, or figure out workarounds so there are fewer documents to score with MaxSim.

The (Partial) Solution: maxsim-cpu

But surely, CPUs can't be that slow? My scoring machine has a whole 48 cores, then it should be able to run scoring faster than in 60ms!?

Thank you for your question, convenient rhetorical question-asker. Indeed, no, it doesn't have to be so slow!

It always comes down to optimisation tradeoffs

A big reason as to why overhead is so big is that MaxSim-style computations, that is, a lot of very small matrices with very low vector dimensions, is quite simply something fairly uncommon and that very few major libraries actively seek to optimise for.

There is a good ecosystem of libraries to speed up CPU computations: ONNX, recent improvements in both PyTorch (better Intel MKL handling...) and JAX (XLA being pretty good at optimising CPU compute nowadays), but they're all (rightfully) much more interested in speeding up the kind of computations you need to run models.

There is actually an entirely separate ecosystem of matrix multiplication libraries which use what are, for the purpose of this blog, essentially magic tricks to speed up maxsim-style operations: they're spearheaded by the very clearly named libxsmm (SMM standing for Small Matrix Multiplication).

In maxsim-cpu, we built on top of libxsmm, and added some additional optimisations to speed things up further, such as fused operations to avoid having to load all the individual distances into memory (which is comparatively very slow, as this visualisation shows), a separate code path to speed things up considerably when handling variable length documents, further optimisations to leverage Apple Silicon-specific optimisations rather than libxsmm, etc...

Gotta go fast

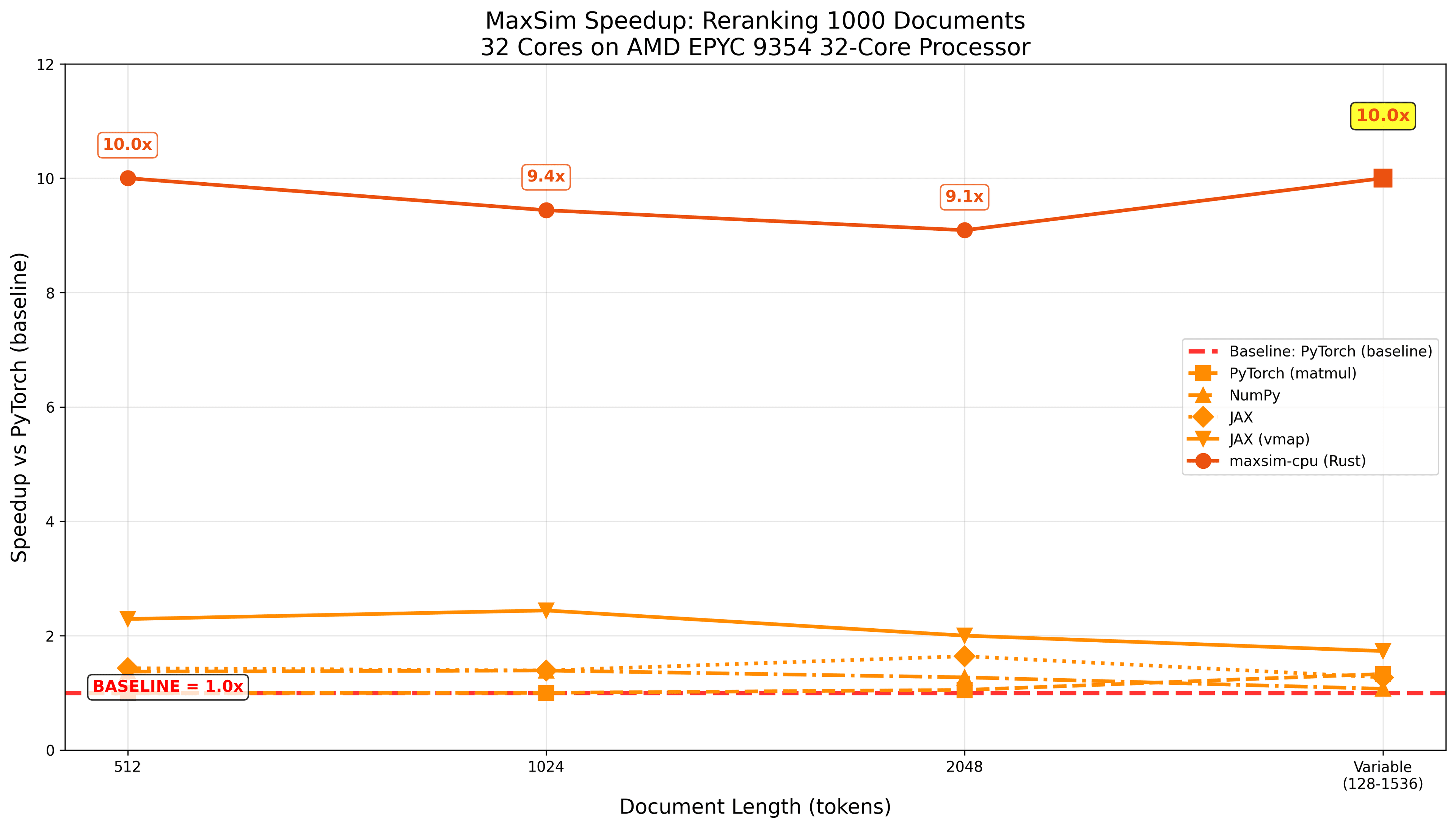
The result is the maxsim-cpu package, written in Rust and exposed as a Python library. In our rapidly ran tests, we observe considerable speed-up over other python packages, while being extremely low-dependency (all you need is numpy and maxsim-cpu itself):

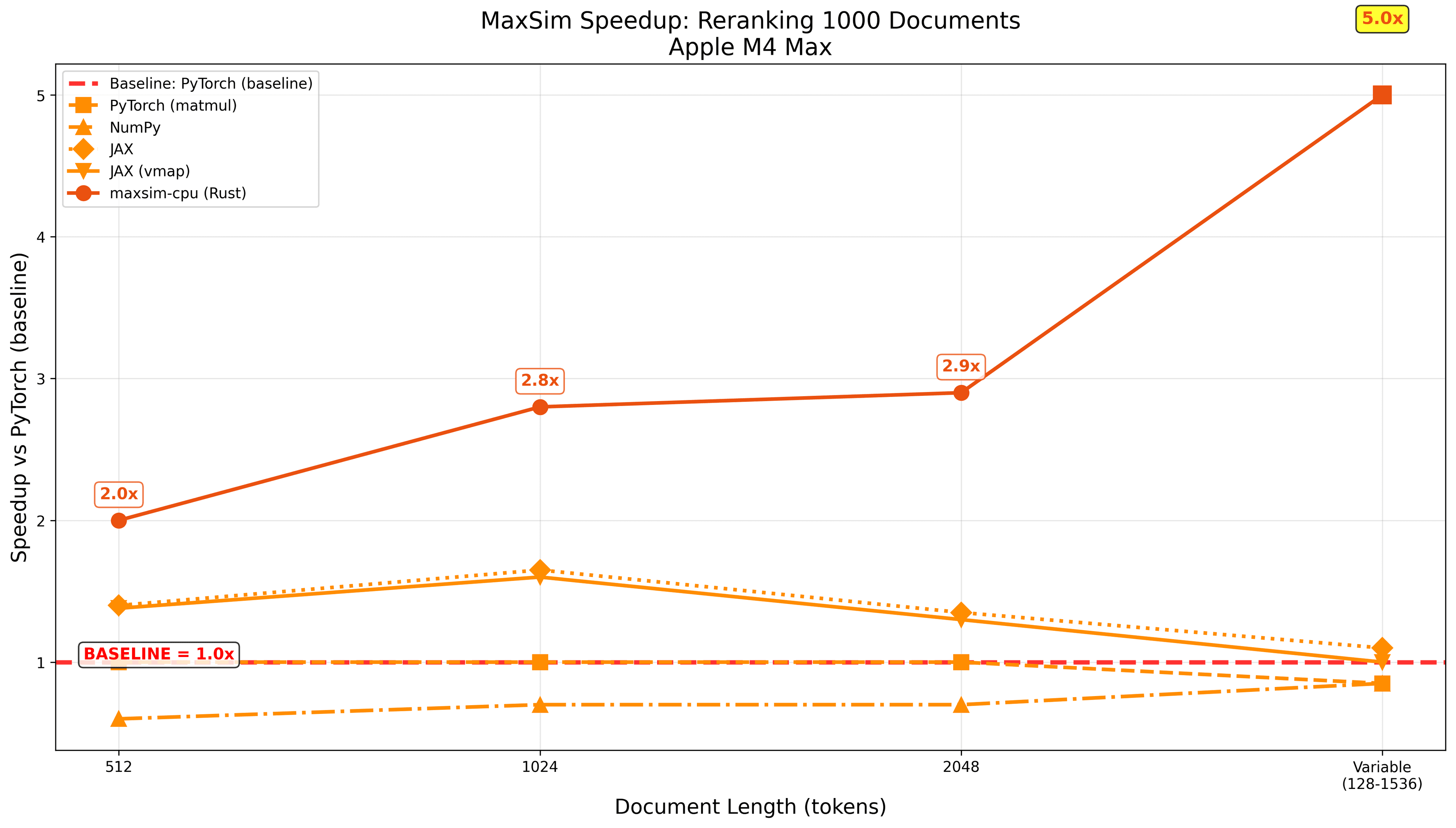
Even on MAC, with much fewer cores and no libxsmm to build on top of, we've observed noticeably speedups, especially on variable batch-size, as our approach allows us to do-away with the dreadfully slow and wasteful Python-based padding operations (note that you could probably optimise those for other libs to also be faster, but it's an annoying bit of engineering to design custom routing logic):

Using maxsim-cpu

The moment you've all been waiting for (or the moment you scrolled to if you're already familiar with MaxSim): how to get your hands on maxsim-cpu? Well, it's quite simple. Below are simple instructions, and you may find more detailed ones as well as the full source code in the GitHub Repository.

Installation

On Linux Machines with x86 processors that support AVX2 instructions (a lot of fancy words to say "Linux machines with a CPU released in the last decade") and Macs with Apple Silicon, you can install it directly from PyPi:

[uv] pip install maxsim-cpu

We do not currently support any other hardware nor do we have plans to, but contributions in this direction (adding AVX512-specific code paths to go even faster or supporting Windows) are welcome and the PRs will be reviewed.

For more detailed installation instructions, including building from source if you'd like to modify the library, head to github.

Usage

The library exposes two methods: maxsim_cpu.maxsim_scores and maxsim_cpu.maxsim_scores_variable, which you should route to depending on the nature of your input: maxsim_scores expects documents to all be the same length while maxsim_scores_variable allows variable length inputs. In all cases, each method expects a single query and its set of candidate documents. Usage is as follows:

import numpy as np
import maxsim_cpu

# Prepare normalized embeddings
query = np.random.randn(32, 128).astype(np.float32)  # [num_query_tokens, dim]

# NOTE: maxsim-cpu expects normalized vectors.
query /= np.linalg.norm(query, axis=1, keepdims=True)

docs = np.random.randn(1000, 512, 128).astype(np.float32)  # [num_docs, doc_len, dim]
# Normalize document embeddings...
docs /= np.linalg.norm(docs, axis=2, keepdims=True)

# Compute MaxSim scores
scores = maxsim_cpu.maxsim_scores(query, docs)  # Returns [num_docs] scores

Swapping in maxsim_scores_variable is straightforward:

import numpy as np
import maxsim_cpu

# Prepare normalized embeddings
query = np.random.randn(32, 128).astype(np.float32)  # [num_query_tokens, dim]

# NOTE: maxsim-cpu expects normalized vectors.
query /= np.linalg.norm(query, axis=1, keepdims=True)

# Create variable-length documents as a list
docs = [
    np.random.randn(np.random.randint(50, 800), 128).astype(np.float32)  # Variable length docs
    for _ in range(1000)
]
# Normalize each document in the list
docs = [doc / np.linalg.norm(doc, axis=1, keepdims=True) for doc in docs]

# Compute MaxSim scores
scores = maxsim_cpu.maxsim_scores_variable(query, docs)  # Returns [num_docs] scores

And that's pretty much it, that's all you need to know to use maxsim-cpu!

Conclusion

This blog post briefly introduces the MaxSim operator as well as our new package, maxsim-cpu. It is a standalone library, meant to do one thing and do it well, and is part of our efforts to open source any individual component we feel might be useful to more than just ourselves, as we previously did with batched and baguetter. We hope it'll be useful to anyone who cares about MaxSim, and that it might even inspire more people to write more optimised versions of commonly used algorithms: search is more relevant than ever, but every small component can still be improved in so many ways.

If figuring out how to create these improvements sounds like something you're interested in, we are currently hiring across all technical positions, don't be shy!

Citation

@online{maxsimcpu2025mxbai,
  title={{maxsim-cpu}: {M}aximising {M}axsim {E}fficiency},
  author={Benjamin Clavié and Sean Lee},
  year={2025},
  url={https://www.mixedbread.com/blog/maxsim-cpu},
}